JS: Binary Search Tree

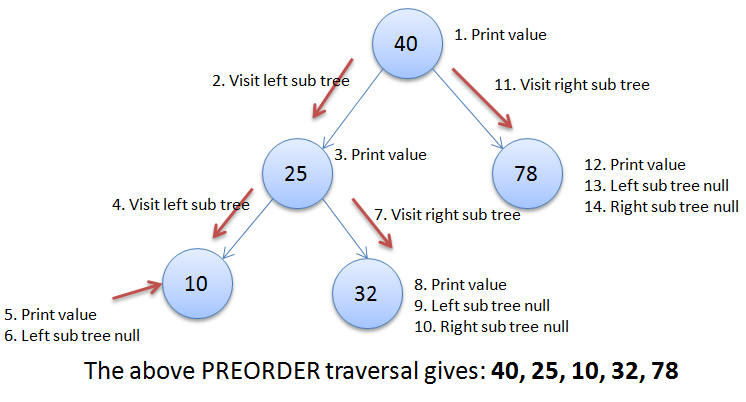
Questions

Binary Search Tree

Question: How would you create a binary search tree?

Answer:

to create a tree you need a node. a node in a tree looks like

function Node(val){
  this.value = val;
  this.left = null;
  this.right = null;
}
        

Create a constructor for binary search tree

function BinarySearchTree(){
  this.root = null;
}
        

Now you need to understand the structure of a binary search tree. For every node value in the left is smaller than the value of the node and value at the right is higher than the value of the root.

so while inserting a value you have to find the appropriate location

BinarySearchTree.prototype.push = function(val){
   var root = this.root;

   if(!root){
      this.root = new Node(val);
      return;
   }

   var currentNode = root;
   var newNode = new Node(val); 

   while(currentNode){
      if(val < currentNode.value){
          if(!currentNode.left){
             currentNode.left = newNode;
             break;
          }
          else{
             currentNode = currentNode.left;
        }
     }
     else{
         if(!currentNode.right){
            currentNode.right = newNode;
            break;
         }
         else{
            currentNode = currentNode.right;
         }
     }
  }

}
        

var bst = new BinarySearchTree();
bst.push(3);
bst.push(2);
bst.push(4);
bst.push(1);
bst.push(5);
        

Breadth First Search

Question: How do you implement Breadth First Search

Answer:

ref: stackoverflow

ref: js algorithms

Depth first search

Question: How to perform in order traversal

function dfs(node){
  if(node){
    console.log(node.value);
    dfs(node.left);
    dfs(node.right);
  }
}
        

In order Traversal

Question:

Answer:

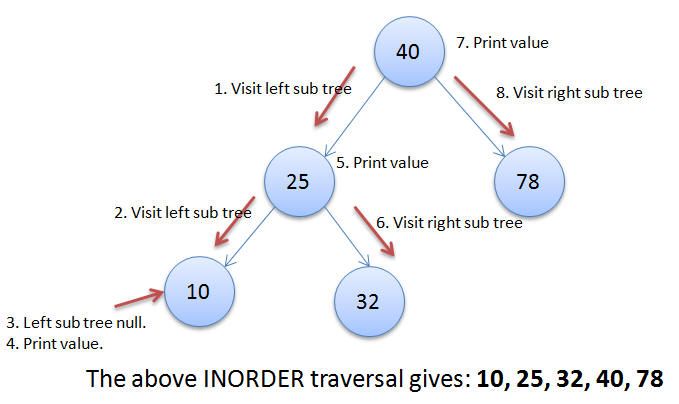
function inorder(node){
   if(node){
      inorder(node.left);
      console.log(node.value);
      inorder(node.right);
   }
}
        

ref: source of image

pre order

//code here
        

ref: wiki pseudocode doesnt work for JavaScript

Post order

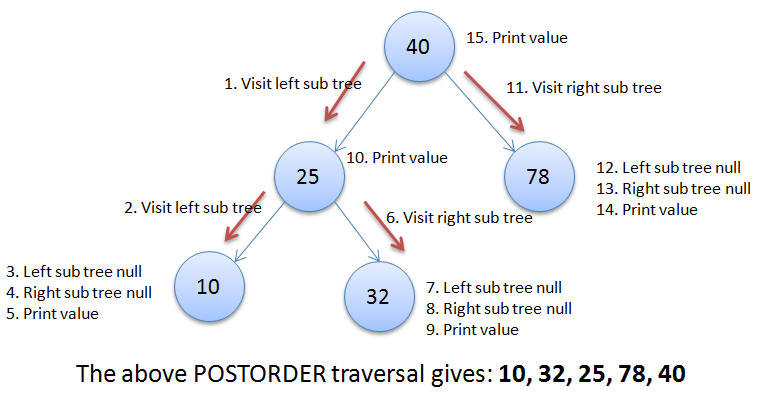
//code here
        

min and max value

Question: How can you find the min value in a bst

finding min is super simple. the go through the left node and left most node is the minimum node

function minNode(node){
   if(!node){
      return 0;
   }
   if(node.left){
     return minNode(node.left)
  }
  return node.value
}
        

Question: How can you find the max value in a bst

function maxNode(node){
   if(!node){
     return 0;
  }
  if(node.right){
     return maxNode(node.right)
  }
  return node.value;
}
        

Balanced and Unbalanced Tree

Question:What is balanced and unbalanced tree

Answer:

1. The left and right subtrees' heights differ by at most one, AND
2. The left subtree is balanced, AND
3. The right subtree is balanced

ref: Get answer from here

Check BST

Question: check a binary tree is BST or not?

Answer:

Simple but wrong approach

Step-1: if node is null, its BST

function isBST(node){
   if(!node){
     return true; 
  }

  if(node.left != null && node.left.value > node.value){ 
    return false;
  }

  if(node.right !=null && node.right.value < node.value) {
    return false;
  }

  if(!isBST(node.left) || !isBST(node.right)) {
    return false;
  }

  return true;  
}
        

The reason this method will generate wrong result is for

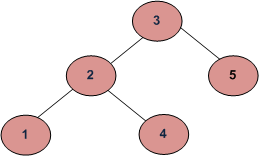
do in order traversal

          //use method 4 in the link below
        

ref: taken from geeksforgeeks

Check balanced

Quetion: How could you check a tree is balanced or not

Answer:

check multiple example whether it is balanced. check balanced tree example

ref: get the answer from here

Height of a tree

function height(node){
   if(!node) return 0;
   var leftHeight = height(node.left);
   var rightHeight = height(node.right);

   return Math.max(leftHeight, rightHeight) + 1;
}
        

print ancestor

Question:

Answer:

function printAncestor(node, target){
   if(!node) return false

   if(node.value == target) return true;
   
   if(printAncestor(node.left, target) || printAncestor(node.rigth, target)){
     console.log(node.value);
     return true;
  }

  return false
}
        

ref: from stack overflow

Doesnt work for intermediate nodes. Debug this

Print all nodes between two nodes

Question:

Answer:

//put the code
        

ref: Get the code form here

common ancestor

this will work for bst only. If you are dealing with binary tree..this needs to be modified

Make this code better

function commonAncestor(node, n1, n2){
   if(!node) return;
   var val = node.value;
   if(n1 < val && n2<val){
     return commonAncestor(node.left, n1, n2);
   }
   if(n1<val && n2<val){
     return commonAncestor(node.right, n1, n2);
  }
  console.log('lowest common ancestor value: ', val);
  return node;
}
        

ref: common ancesotr

coomon ancestor for binary tree

function commonAncestorBT(node, n1, n2){
   if(!node) return;
   var val = node.value;
   if(n1 == val || n2 ==val){
     return node;
   }
   var left = commonAncestorBT(node.left, n1, n2);
   var right = commonAncestorBT(node.right, n1, n2);
   if(left && right){
     return node;
  }
  return (left) ? left : right;
}
        

ref: try pavels blog

ref: common ancestor for binary tree

check bst is height balanced

Qustion

ref: get code from here

Top view

bottom view

leftview

ref: bst left view

Right view

ref: print right view

Merge two BST

ref: merge two bst

convert binary to BST

ref: binary tree to bst

Check Sub tree

ref: check subtree

Diagonal Sum

ref: gfg

Self Balancing or Height Balanced Tree

Question:

Answer:

A binary tree whose height of the left subtree and height of the right subtree differ at most one.

AVL Tree

Question:

Answer:

It is Self balancing binary search tree. This means in an AVL tree, heights of two child subtrees of any node differ by at most one. If at any time if heights differ more than one, re-balancing is done to restore the height balance property.

Lookup, insertion and deletion all takes O(logn) in average and worst case

Insert, delete Into AVL

Red Black Tree

Question:

Answer:A red-black tree is a binary search tree with one extra attribute for each node: the colour, which is either red or black.

• Every node is either red or black.
• Every leaf (NULL) is black.
• If a node is red, then both its children are black. However, two black node may be adjacent
• Every simple path from a node to a descendant leaf contains the same number of black nodes.
• Root node will always be black

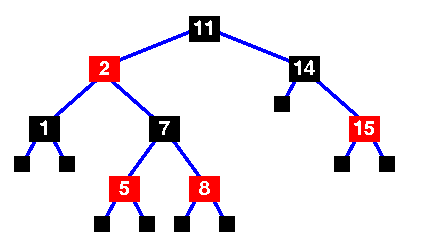
ref: Red Black Trees

Insert into Red Black Tree

Questions list

from cracking the coding interview

• check binary tree is balanced
• two nodes are cusin
• lowest common ancestor
• k th smalled node
• in order successor and precessor
• maximum path between two nodes
• all nodes of k distance
• vertical order
• nodes that doesnt have siblings
• bst to doubly linked list
• deepest left node
• check leaves
• sum of odd levels and even levels node
• isporphisom: dont know what is this
• pair with a given sum
• floor and ceil of bst
• two nodes swapped, correct bst
• check complete or not
• max width of bst
• all root to leaf path
• BST from sorted array
• From BST, linked list for each level
• check binary tree is BST
• next node (in-order successor) of BST
• First common ancestor of two nodes in BT
• Very large two BT. check one is sub tree of another
• all path that sums to a number in BT
• carzy for code list of tree questions
• geeks for geeks questions
• glassdoor questions
• you tube got some questions as well
• career cup list of question

Express anger!